Primjene teorije grafova
Ravni grafikoni
Za graf G kaže se da je ravan ako ga se može prikazati na ravnini na takav način da su vrhovi različite točke, a rubovi su jednostavne krivulje, a ne nalaze se dva ruba jedan s drugim osim na njihovim terminalima. Na primjer, K 4, kompletan graf na četiri vrha, je ravan, kao što prikazuje slika 4A.

Za dva se grafa kaže da su homeomorfni ako se oba mogu dobiti iz istog grafa prema pododjeljcima rubova. Na primjer, grafikoni na slici 4A i slici 4B su homeomorfni.
K m, n graf je graf za koji se skup vrhova može podijeliti u dva podskupina, jedan s m vrhovima i drugi s n vrhova. Svaka dva vrha istog podskupa nisu povezana, dok su svaka dva vrška različitih podskupova susjedna. Poljski matematičar Kazimierz Kuratowski 1930. dokazao je sljedeću poznatu teoremu:
Nužan i dovoljan uvjet graf G da bude ravna je da ne sadrži graf homeomorphic nijednom K 5 ili K 3,3 prikazano na slici 5,

Elementarna kontrakcija graf G je transformacija G na novi grafu G 1, tako da se dva susjedna vrha U i v G zamijenjen novim vrh w u G 1 i m je susjedan na G 1 sve vrhove na koja je u ili U susjedna u G. Za graf G * kaže se da je kontrakcija G ako se G iz G može dobiti nizom elementarnih kontrakcija. Slijedi još jedna karakterizacija ravninskog grafa uslijed njemačkog matematičara K. Wagnera 1937. godine.
Graf je ravan ako i samo ako nije kontraktibilan za K 5 ili K 3,3.
Problem s mapom u četiri boje
Više od jednog stoljeća rješenje problema s kartama u četiri boje izbjegavalo je svakog analitičara koji je to pokušao. Problem je možda privukao Möbiusovu pažnju, ali čini se da je prva pisana referenca na njega jedno pismo jednog Francisca Guthrieja njegovom bratu, studentu Augustusa De Morgana, 1852. godine.
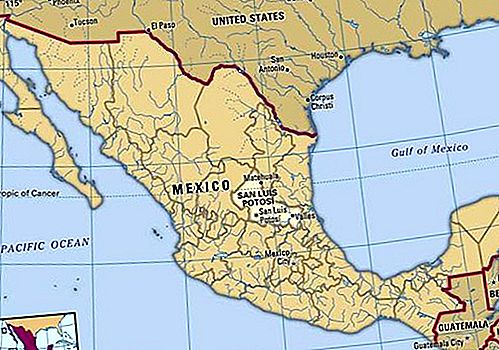
Problem se odnosi na ravninske karte - to jest podjele ravnine na nepregledna područja koja su omeđena jednostavnim zatvorenim krivuljama. Na geografskim kartama empirijski je opaženo, u toliko posebnih slučajeva koliko je pokušano, da su potrebne najmanje četiri boje kako bi se regije obojile tako da dvije regije koje imaju zajedničku granicu uvijek budu obojene različito i određeni slučajevi da su potrebne najmanje četiri boje. (Regije koje se sastaju samo u određenom trenutku, poput država Kolorado i Arizona u Sjedinjenim Državama, ne smatraju se zajedničkom granicom). Formalizacija ovog empirijskog opažanja čini ono što se naziva "teoremom u četiri boje." Problem je dokazati ili opovrgnuti tvrdnju da je to slučaj za svaku ravninsku kartu. Da tri boje neće biti dovoljne, lako je pokazati, dok je dovoljnost pet boja dokazao 1890. godine britanski matematičar PJ Heawood.
Godine 1879. Englez AB Kempe predložio je rješenje problema u četiri boje. Iako je Heawood pokazao da je Kempeova tvrdnja pogrešna, dva su njena koncepta u kasnijoj istrazi urodila plodom. Jedna od njih, nazvana neizbježnost, ispravno navodi nemogućnost izrade karte na kojoj je svaka od četiri konfiguracije odsutna (te se konfiguracije sastoje od regije s dva susjeda, jedna s tri, jedna s četiri i jedna s pet). Drugi koncept, onaj reducibilnosti, dobio je ime po valjanom dokazu Kempea da ako postoji karta koja zahtijeva najmanje pet boja i koja sadrži regiju s četiri (ili tri ili dvije) susjede, tada mora postojati karta koja zahtijeva pet boje za manji broj regija. Pokušaj Kempea da dokaže reduciranost karte koja sadrži regiju s pet susjeda bio je pogrešan, ali to je ispravljeno u dokazu koji su 1976. godine objavili Kenneth Appel i Wolfgang Haken iz Sjedinjenih Država. Njihov dokaz privukao je neke kritike jer je zahtijevala procjena 1.936 različitih slučajeva, od kojih je svaki uključivao čak 500.000 logičkih operacija. Appel, Haken i njihovi suradnici osmislili su programe koji su velikom digitalnom računalu omogućili rukovanje tim detaljima. Računalu je bilo potrebno više od 1000 sati za obavljanje zadatka, a rezultirajući formalni dokaz dugačak je nekoliko stotina stranica.
Eulerijski ciklusi i problem Königsbergovog mosta
Multigraf G sastoji se od ne-praznog skupa V (G) vrhova i podskupine E (G) skupa neuređenih parova različitih elemenata V (G) s frekvencijom f ≥ 1 pričvršćenim za svaki par. Ako par (x 1, x 2) s frekvencijom f pripada E (G), tada su vrhovi x 1 i x 2 spojeni f ivicama.
Eulerov ciklus ciklusa G je zatvoreni lanac u kojem se svaki rub pojavljuje točno jednom. Euler je pokazao da multigraf posjeduje eulerov ciklus ako i samo ako je povezan (osim izoliranih točaka), a broj vrhova neparnog stupnja je ili nula ili dva.
Prvi je problem nastao na sljedeći način. Rijeka Pregel, nastala sutokom dviju grana, prolazi kroz grad Königsberg i protiče s obje strane otoka Kneiphof. Bilo je sedam mostova, kao što je prikazano na slici 6A. Građani su se pitali je li moguće ići jednom u šetnju i prijeći svaki most. To je ekvivalentno pronalasku Eulerovog ciklusa za multigraf na slici 6B. Euler je pokazao da je nemoguće jer postoje četiri vrha neparnog reda.